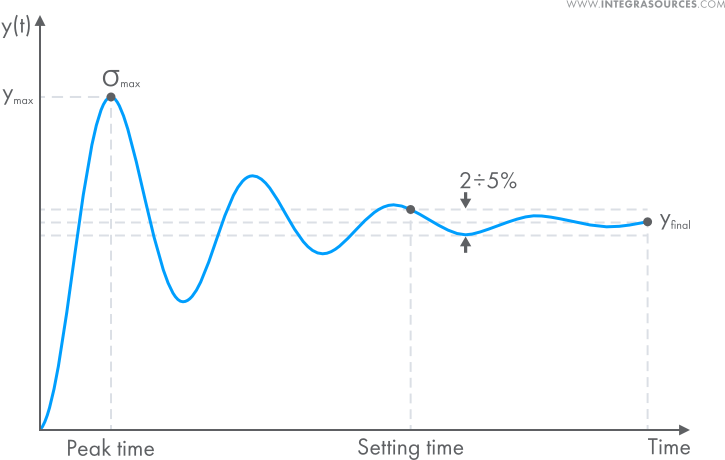
Proportional–Integral–Derivative (PID) controllers are widely used across many fields, including motor control, flight systems, and power management. They are essential in electric vehicles and are commonly found in temperature and humidity control systems within manufacturing, chemical, and pharmaceutical industries. PID controllers also play a key role in power electronics, such as in converters and industrial furnaces, making them vital for automation in modern manufacturing processes.

The PID algorithm uses three components—proportional, integral, and derivative—to generate a control signal. Each component is multiplied by a gain that adjusts its impact on the output. Engineers can fine-tune these gains to optimize system performance. For more information on the basics of PID controllers, refer to our previous article.

At Integra Sources, we have extensive experience designing and implementing PID controllers in various applications. If your project involves automation, PID control could be an excellent solution. Contact us to discuss how we can help with your specific needs.

While PID controllers can be tuned intuitively, the process is often challenging, especially for those new to control systems. In this article, we will explore the nuances of PID gain tuning and how it affects system performance. Let’s start by looking at the origins of these controllers.

History of PID Controllers

Although there is no official patent for the first PID controller, early engineers used similar concepts in various applications. For example, the "automatic helmsman" on ships was essentially a form of PID control. The concept gained more attention when the airplane autopilot was demonstrated in 1914, showing that aircraft could fly without manual input.

This demonstration sparked interest in automated control systems, leading to the development of various PID implementations. However, differences in design led to vendor lock-in, making it difficult for users to switch between manufacturers. Despite this, PID controllers became widely adopted due to their effectiveness and adaptability.

Interestingly, the mathematical model of the PID controller was not fully developed until over a decade after its initial use. This means that early PID systems were based on practical engineering intuition rather than theoretical optimization.

Transient Response Performance Indicators

To understand what makes a PID controller well-tuned, we need to consider transient response indicators. These metrics help evaluate how quickly and accurately a system responds to changes. Common indicators include settling time, overshoot, and steady-state error.

Settling time refers to how long it takes for a system's output to stabilize within a certain range of its final value. Overshoot measures how much the system exceeds its target before stabilizing. Steady-state error shows the difference between the desired and actual values once the system has settled.

These indicators vary depending on the application, but they provide a standardized way to assess controller performance. Understanding them is crucial for effective tuning.

Representations of PID Gains

Each term in the PID equation is associated with a gain that determines its influence on the system. The proportional gain (Kp) affects the current error, the integral gain (Ki or Ti) addresses accumulated error, and the derivative gain (Kd) predicts future errors based on the rate of change.

There are different ways to represent these gains, which can sometimes lead to confusion. For instance, the integral gain may be expressed as Ki (common in academic settings) or Ti (more common in engineering). The relationship between them is defined by the formula: Ki = 1/Ti.

The derivative gain (Kd) is often represented similarly across different systems, though its behavior can vary depending on the implementation. It's important to note that increasing Kd can amplify noise, so careful tuning is necessary to maintain stability.

Forms of PID Controller

PID controllers come in different forms, each with its own advantages and challenges. The two most common forms are the parallel and series configurations. The parallel form is widely used in academic research, while the series form is more popular in practical engineering applications.

When tuning a PID controller, it's important to understand the form being used. The series configuration often provides smoother tuning and better stability, making it a preferred choice for embedded systems and real-time applications.

How PID Gains Affect the Transient Response

Tuning PID gains directly impacts the system's transient response. Increasing the proportional gain reduces the steady-state error but can lead to increased overshoot. The integral gain helps eliminate steady-state error but may increase settling time and oscillation. The derivative gain improves stability but can make the system more sensitive to noise.

By analyzing the surface plots of settling time and overshoot, it becomes clear that the series form of the PID controller is easier to tune. This is because the minimum values are more distinct, allowing engineers to adjust only one gain at a time for optimal results.

Conclusion

Tuning a PID controller requires both technical knowledge and practical experience. The different forms of PID representation and the complexity of gain adjustment make this task challenging for beginners. However, with proper understanding and tools, it is possible to achieve excellent system performance.

If you're working on an automation project and need expert guidance, our team at Integra Sources is here to help. We specialize in developing control systems and can assist you in selecting the right PID configuration for your application.